邏輯島遊戲通關攻略 詳細規則及組合技巧一覽

邏輯島遊戲v1.0.3

類型：休閑益智

大小：37.62MB

評分：5.0

平台：

標簽：數學解謎趣味連線

立即下載

邏輯島遊戲怎麼玩？有哪些規則？邏輯島遊戲是個趣味搭橋遊戲，每個橋搭建需要一定的方法技巧才可哦，掌握好規律還有順序即可搭橋成功，詳細的玩法技巧下麵來告訴給大家吧~

邏輯島遊戲通關攻略

邏輯島玩法為Hashi wo Kakero（意為建造橋梁、搭橋，簡稱Hashi），遊戲規則為數字代表島嶼，玩家在島嶼之間搭橋，最終要符合以下要求

隻能豎直或者水平方向上連接

橋不能相交

一對島嶼之間最多隻能搭兩座橋

島嶼上數字與連向該島嶼的橋數量一致

所有島嶼之間必須直接或間接相連（即從任意一個島嶼，可通過橋前往任意的另一個島嶼）

因為這些限製，可以得出不少規律，分為

固定模式：觀察一個島嶼，根據與該島嶼相鄰（上下左右4方向）的島嶼情況，以及島嶼間最多兩座橋的規律，推斷橋的數量

孤島排除模式：觀察一個島嶼，根據與該島嶼相鄰（上下左右4方向）的島嶼情況，以及所有島嶼必須連通的規律，推斷橋的數量

排除法：假設某方向沒有橋，推導得出錯誤結果，從而斷定某方向上有橋
全分支交集法：某種情況的所有可能性都推導出某一部分共同結果，則該結果為正確解

閉環分析法：根據閉環存在的規律，推導出非閉環與環外連接情況來確定橋

要注意的是，當前版本（版本號1.3.4）的謎題中，絕大部分（甚至可能全部），隻需要前兩類規律即可解出來（不過多了解點規律對凹速度或許有用？霧）

注：個人命名方法，可能聽起來比較怪，問就是想不到好名字
一、固定模式

說明：使用如41**格式來表示，第一個數字表示要觀察的島嶼的數字，後麵數字或*代表相鄰島嶼可搭橋數量（數字-已搭橋數量），*代表可搭橋數量≥2，

這些固定模式不建議硬背，理解中記憶，列出來是為了防遺漏，實際上因為要減去橋的數量、距離可能很遠、附近島嶼較多等原因，就算是簡單的模式，也可能很難發現。

二、孤島排除模式

因為規則中有要全連通的要求，所以可以通過排除孤島來確定連線，與上麵固定模式不同，這裏數字不能簡單用原數字-已連橋數量，

還需要滿足與除了*以外方向為不可再向外連接的孤島狀態。規律為除了某個方向外其他島嶼數字可搭橋數量加起來等於島嶼數字，理解中記憶。

三、排除法

通過假設某情況，根據該情況推導產生錯誤結果時，可以排除掉這種情況，此時有可能可以得出某些必定存在的橋，下麵隻是舉例一些簡單的情況，複雜情況可能需要自己分析，a向b表示可能存在a個可搭橋方向的數字b島嶼3。此處*可能為數字1。

2向1（1**）

數字1的島嶼必定往其中一個方向搭橋，記兩個方向分別為 a b，假設a方向有橋，發現錯誤，則b方向搭1座橋，其他方向同理，假如都未出現錯誤，則不確定。

2向2（2**）

數字2的島嶼必至少往其中一個方向搭橋，記兩個方向分別為 a b，假設a方向有橋，發現錯誤，則b方向搭2座橋，其他方向同理，假如都未出現錯誤，則不確定。

3向3（3***）

數字3的島嶼至少往2個方向搭橋，記三個方向分別為a b c，假設a b方向有橋，推導出錯誤結果，那麼c方向至少有1座橋，其他方向同理。

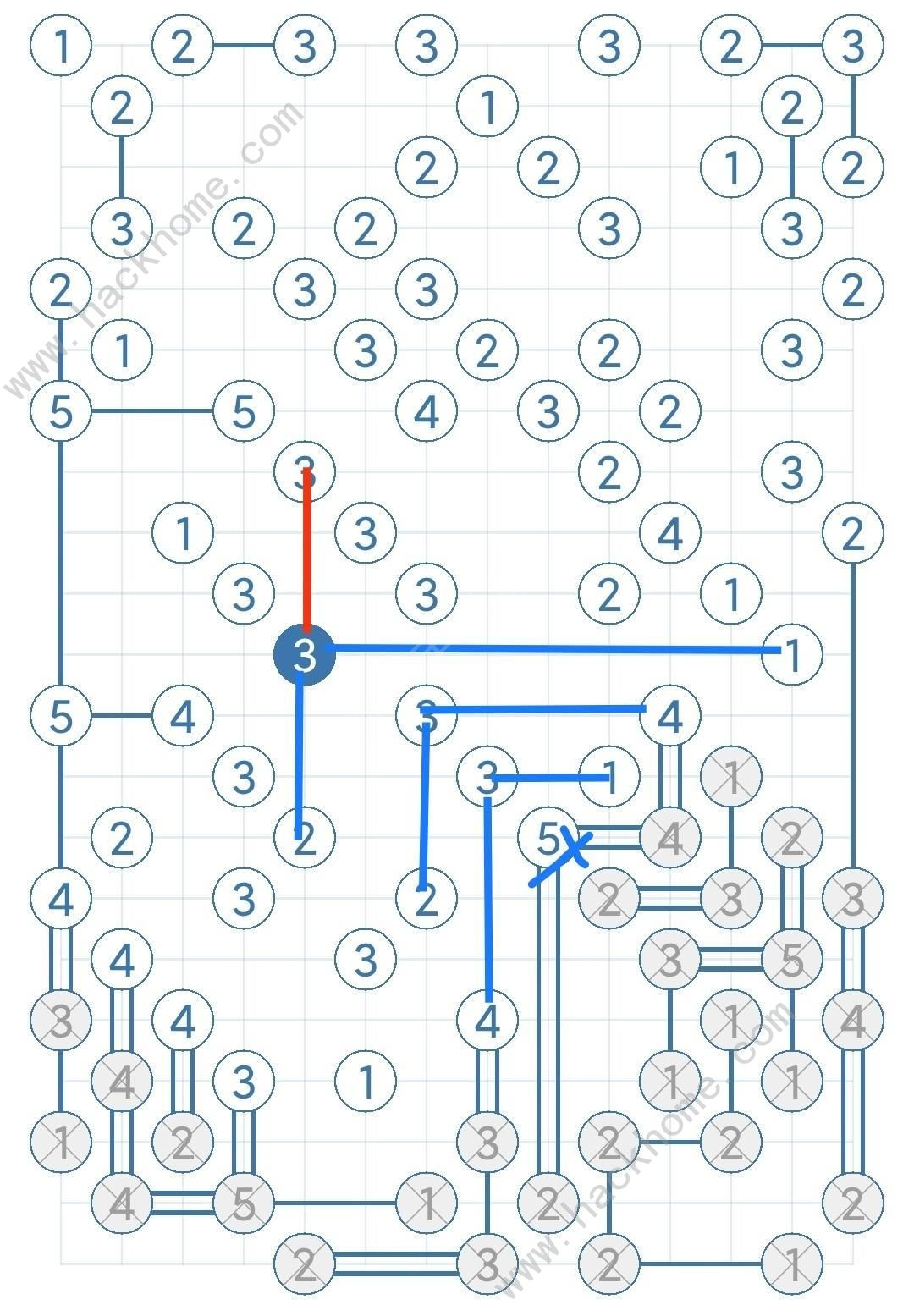
藍色為假設推導方向，紅色為推導結果

3向4（4***）

數字4的島嶼至少往2個方向搭橋，記三個方向分別為a b c，假設a b方向有橋，推導出錯誤結果，那麼c方向必有有2座橋，其他方向同理

4向5（5****）

數字5的島嶼至少往3個方向搭橋，記四個方向分別為a b c d，假設某a b 方向有橋，推導出錯誤結果，那麼c d方向分別至少有一座橋，其他方向同理

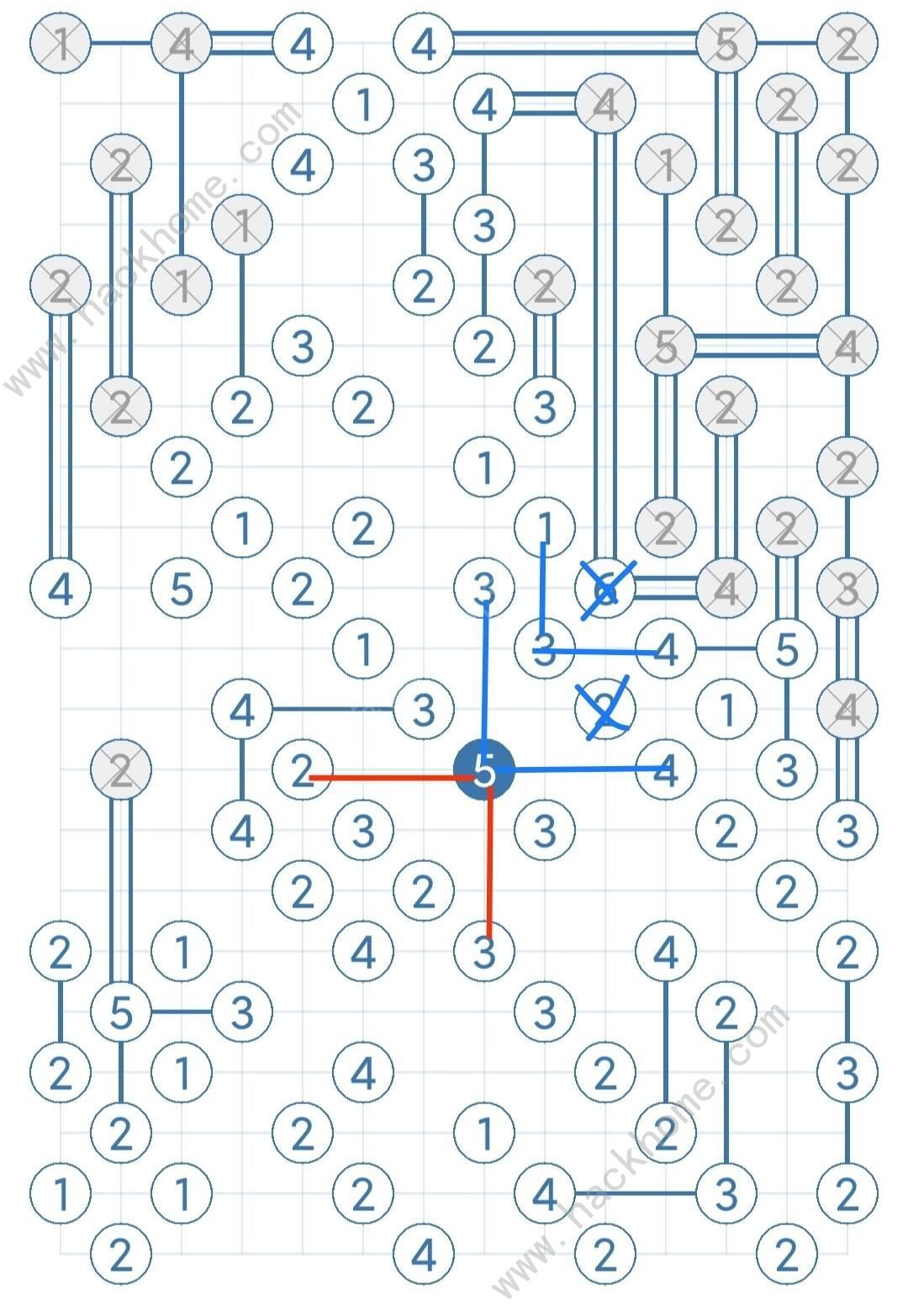
4向6（6****）

數字6的島嶼至少往3個方向搭橋，記四個方向分別為a b c d，假設某a b 方向有橋，推導出錯誤結果，那麼c d方向分別必定搭2座橋，其他方向同理

等效情況

例如41***，除了數字1的方向外三個方向至少搭3座橋，因此至少往兩個方向搭橋，與3**情況一樣

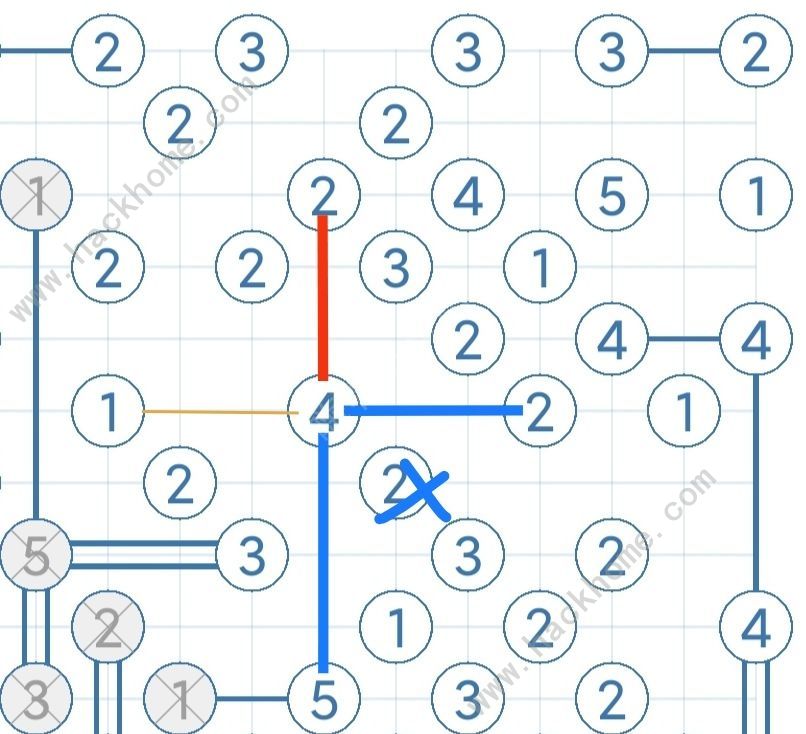
注意：此圖為初版未保證連通和唯一解時的非標準Hashi謎題的圖，因此結果會出現多解或孤島為正常現象。

四、全分支交集

假如某處有3種可能情況，且為所有可能性（並集為全集），這3種情況得出的推導結果有交集，則此交集為正確解。

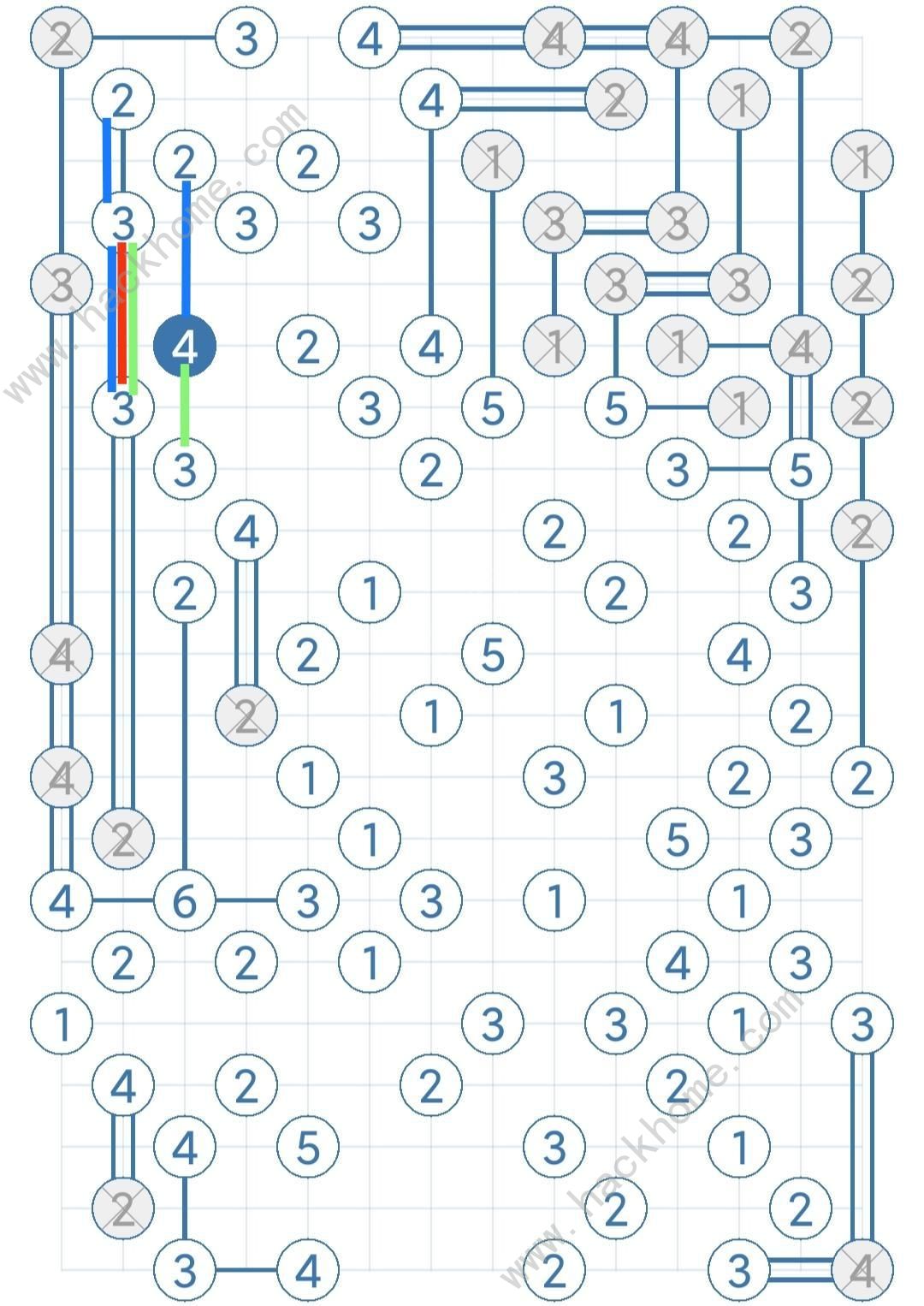
舊版本圖注意事項同上

數字為4的島嶼可與三個方向連線，上下方向上至少一個方向有橋，因此有三種可能，向上有橋，向下有橋，或者都有橋，圖上藍色和綠色分別代表兩種可能，上下都有橋的情況與藍色類似，就不畫了，可以看出共同結果為紅線的兩個3相連因此紅線為正確解。

五、閉環分析法

將一係列島嶼連成一個環，如果該環上島嶼均不能再繼續往環外搭橋，則稱該環為閉環，閉環與環上橋的會有一定規律，通過這些規律可以進行推導。

閉環上每座橋會為環內兩個島嶼數字分別+1，因此閉環內島嶼數字總和減去向環外搭橋數量結果一定為偶數。

假如閉環上除了相鄰島嶼以外的島嶼均無法連接，且環內島嶼數量為偶數，將相鄰島嶼分開，相間島嶼組成組一起，分成兩組，因為環上的橋必定是兩組島嶼之間進行的連接，

所以兩組島嶼數字總和（減去與環外搭橋數量）相等。特殊的，假如環內不同組的島嶼之間存在其他連接，不破壞橋必定是兩組島嶼之間進行連接的規律，因此此規律仍然適用。

根據上麵規律，假如一個環，與環外存在較少連接點時，可能可以推導出該連接點的搭橋情況，如下圖。

舊版本圖注意事項同上

紅色圈起來的環（左上開始順時針4342，減去往外搭橋數量為3342）），按相間島嶼分成兩組，左上4和右下4一組，左下2和右上3一組，

環上存在兩個外部連接點為左上和右下，都在第一組，根據第一組數字總和（減去向外搭橋數量）為7，第二組數字總和為5，可知第一組必定向外搭2座橋，

再根據左上和右下分別可最多可向外搭1座橋，因此左上和右下分別向外搭1座橋。順便一說，將數字減去環內已搭橋數量（2121）結果也是一樣的。

另外要注意的是，環內部可能存在島嶼，隻要不能與環上島嶼搭橋就不影響，有時候可用於進行分析的環可能並不好找。

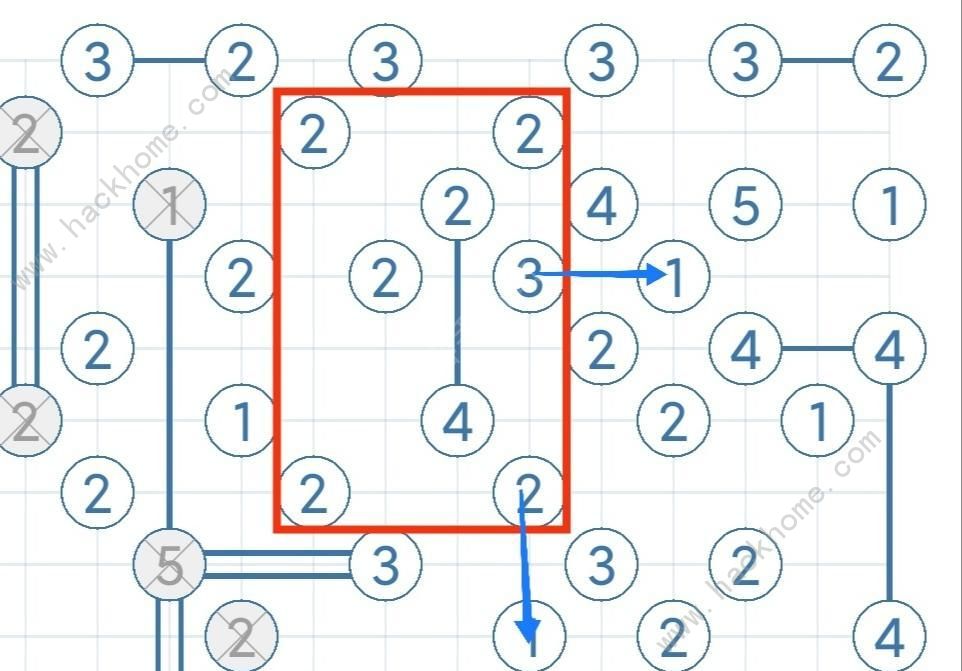
舊版本圖注意事項同上

此圖紅色的環隻存在藍色箭頭兩個連接點，很好分析，但是正常較難發現（非標準Hashi謎題圖注意事項同上圖）。