類型:休閑益智
大小:652.08MB
評分:10
平台:

我的勇者新版本賭狗該怎麼玩,相信很多玩家都不清楚,那麼現版本賭狗有什麼收益,去舊版本對比如何呢,下麵一起來看看詳細的攻略內容。

第一部分、賭狗收益
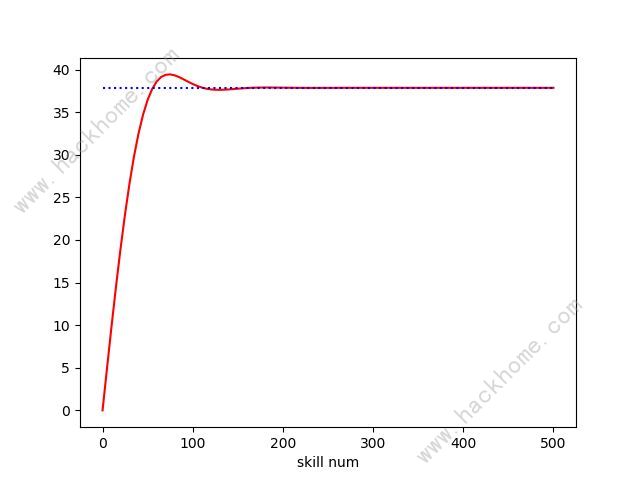
以下所有數據圖均為 釋放技能次數與賭狗期望增傷的關係
1、新版賭狗
?新版賭狗對於一場戰鬥釋放技能次數超過100次的職業,可以認為期望收益為37.8502。
?對於技能釋放次數在50-100之間的職業賭狗收益將會高於37.8502,最高會接近於40。比如一些技能算作普攻的職業,技能釋放頻率低,世界boss賭狗收益會超過其他職業一些。技能釋放頻率低不再是劣勢
?另外對於新賭狗,層數低的時候釋放無用的技能疊層數,層數高的時候隻放高傷害技能會帶來比老版本賭狗更大的收益(其實這個和為什麼技能釋放次數50-100之間的職業賭狗收益會大於37.85是同一個原因)
?其次,新賭狗收益的方差會遠小於老賭狗,超級歐皇和非酋的情況會少很多。
2、老版賭狗
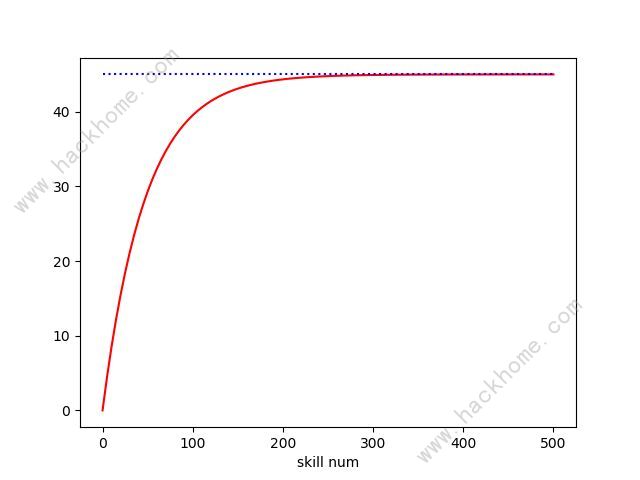
50%
我支持
0
50%
我反對
0
 音樂盒子模組下載安裝手機版最新 v1.0.5休閑益智2024/6/21
音樂盒子模組下載安裝手機版最新 v1.0.5休閑益智2024/6/21 奇跡特攻隊安卓手機版 v1.0.0動作射擊2024/6/21
奇跡特攻隊安卓手機版 v1.0.0動作射擊2024/6/21 文字修仙傳微信遊戲內置菜單版 v1.0休閑益智2024/6/21
文字修仙傳微信遊戲內置菜單版 v1.0休閑益智2024/6/21 萌寵戰鬥吧下載安裝最新版 v2.0角色扮演2024/6/21
萌寵戰鬥吧下載安裝最新版 v2.0角色扮演2024/6/21 狼魂暗黑專屬官方安卓版下載 v4.4.8角色扮演2024/6/21
狼魂暗黑專屬官方安卓版下載 v4.4.8角色扮演2024/6/21 一念仙域手遊下載正版 v1.0角色扮演2024/6/21
一念仙域手遊下載正版 v1.0角色扮演2024/6/21